Blog

O ebook Julia com Física: uma introdução foi lançado!

Adeil Araújo e Meirivâni Oliveira, Julia com Física: uma introdução, Seduc - CE, setembro de 2023.

Animações em Julia com o Javis.jl

Seguindo este tutorial passo a passo você obterá, ao final, a seguinte animação:

Abaixo, apresentamos o código para a animação acima. Mas, antes de dar um Ctrl+C, CtrL+V para um ambiente Julia, como o Jupyter por exemplo, vamos entender os principais pontos do código?

Nota 1: Teste o código a seguir no REPL do Julia ou no Jupyter instalado em sua máquina. Não obtivemos êxito em ambientes online.

using Javis

function ground(args...)
    background("black") # Cor de fundo da tela
    sethue("black") # cor da caneta
end

function object(p=O, color="black", radius=1)
    sethue(color)
    circle(p, radius, :fill)
    return p
end

function path!(points, pos, color)
    sethue(color)
    push!(points, pos) # adiciona posição aos pontos.
    circle.(points, 2, :fill) # desenha círculos para cada ponto usando broadcasting
end

meuvideo = Video(700, 700)

trajetoria_da_terra = Point[]
trajetoria_da_lua = Point[]

Background(1:500, ground)
sol = Object((args...)->object(O, "yellow",35), Point(0,0))
terra = Object(1:500, (args...)->object(O, "blue",15), Point(200,0))
act!(terra, Action(anim_rotate_around(2π, O)))
lua = Object(1:500, (args...)->object(O, "gray",5), Point(150,30))
act!(lua, Action(anim_rotate_around(24π, terra)))
Object(1:500, (args...)->path!(trajetoria_da_terra, pos(terra), "blue"))
Object(1:500, (args...)->path!(trajetoria_da_lua, pos(lua), "gray"))

render(meuvideo; pathname="orbita_oficial1.gif")

Então, bora lá!

O primeiro passo é fazer a instalação do pacote^[1] Javis.jl. Se você estiver usando o Jupyter insira os comandos:

using Pkg
Pkg.add("Javis")

Nota 2: Este passo não consta no código acima. Ele será necessário apenas na primeira vez que você for usar o pacote em seu computador.

Após a instalação precisamos carregar o pacote para o nosso código. Para isso, digite o comando abaixo:

using Javis

Pronto! Com o pacote instalado e devidamente carregado, podemos iniciar a construção da nossa animação.

Nossa primeira tarefa na construção da animação é definir a função^[2] ground. Ela definirá o fundo da animação (background) e a cor da "caneta" (pen) como preto. Observe o código abaixo:

function ground(args...)
    background("black") # cor de fundo da tela.
    sethue("black") # cor da caneta
end

Você pode estar se perguntado porque args... na primeira linha. Vamos te explicar. Cada função definida pelo usuário recebe três argumentos: video (estrutura do vídeo), object (estrutura do objeto) e frame (o número de quadros atuais) fornecidos pelo Javis.jl.

Embora esses argumentos sejam irrelevantes para a função ground, precisamos escrever args...para que Julia saiba que temos uma função que aceita esses três argumentos. Quanto ao ... significa basicamente quantos argumentos você quiser.

A seguir criamos a função object, ela define uma cor para os círculos, um raio padrão de tamanho 1 e os desenha adequadamente. Veja o código abaixo:

function object(p=O, color="black", radius=1)
    sethue(color)
    circle(p, radius, :fill)
    return p
end

Na função acima radius é o raio da bola,em nossa simulação criaremos 3 bolas de raios de tamanhos diferentes e :fill preenche a bola com a cor que definirmos.

A última função que criaremos em nosso código é a função path!. Ela desenha a trajetória das bolas. Veja o código abaixo:

function path!(points, pos, color)
    sethue(color)
    push!(points, pos) # adiciona pos aos pontos
    circle.(points, 2, :fill) # desenha círculos para cada ponto usando broadcasting
end

Nota 3: O pos assume a posição de uma determinada bola e passa-o como argumento para a função path!.

Nota 4: O conceito de broadcasting está descrito em detalhes no capítulo 7 do livro Julia com Física: Uma Introdução.

A seguir criamos a variável meuvideo e atribuímos a ela um video, ele define a tela de vídeo para a animação. Aqui nossa tela possui 700 pixels de largura por 700 pixels de altura.

myvideo = Video(700, 700) # 700 x 700 (largura x altura)

Cada objeto ou ação que criamos durante o código é adicionado ao meuvideo.

A seguir criamos duas variáveis trajetoria_da_terra e trajetoria_da_lua que armazenarão em um vetor ^[3] os pontos da trajetória das bolas azul e cinza.

trajetoria_da_terra = Point[]
trajetoria_da_lua = Point[]

Logo após, usamos Background para especificar que a função ground será aplicada a todos os objetos descritos posteriormente.

Background(1:500, ground)

o valor $1:500$, se refere a quantidade de quadro da animação de 1 a 500 e está relacionado também a veocidade da animação. Varie o valor 500 para mais e para menos para ver o que acontece. Vamos dar spoiler: Quando diminuímos a taxa para, por exemplo, 1:200 a animação fica mais rápida.

Abaixo descrevemos o código para a variável sol. Ela representa o Sol e estará localizada no centro da animação e não possuirá movimento.

sol = Object((args...)->object(O, "yellow",35), Point(0,0))

Nosso objeto solterá cor amarela e radio de valor 35no trecho de código acima se refere ao raio do SOl.

Posteriormente definimos o objeto terra, que representará o planeta Terra em nossa animação.

terra = Object(1:500, (args...)->object(O, "blue",15), Point(200,0))
act!(terra, Action(anim_rotate_around(2π, O)))

Perceba que a cor e a posição da variável terra são definidos na função anônima ^[4] (args...)->object(O, "blue",15), Point(200,0)).O valor´15se refere ao raio da terra e Point(200,0) significa que terra estará localizada à 200 pixels da origem na direção x.

Logo abaixo de terra aparece pela primeira vez o método act!.

O trecho de códigoact!(terra, Action(anim_rotate_around(2π, O))) fará com que terragire em um ângulo de $2π$ em torno do centro da animação.

Abaixo definimos o lua, ela representará a Lua em nossa simulação.

lua = Object(1:500, (args...)->object(O, "gray",5), Point(150,30))
act!(lua, Action(anim_rotate_around(24π, terra)))

Perceba que assim como ocorreu com terra a cor e a posição da lua também são definidos na função anônima (args...)->object(O, "gray",5), Point(150,30)). Onde o valor 5 se refere ao raio da lua e Point(150,30) significa que a lua estará localizada à 150 pixels da origem na direção x e 30 pixels da origem na direção y.

O trecho de código act!(lua, Action(anim_rotate_around(24π, terra))) diz que lua irá girar em um ângulo de $24π$ em torno da terra. Isso fará com que nossa Lua descreva uma espécie de espiral para contornar a Terra. Tente modificar esse valor para ver o que acontece.

A seguir vemos que os objetos trajetoria_da_terrae trajetoria_da_lua(caminho da terra e caminho delua) são definidos nas funções anônimas (args...)->path!(trajetoria_da_terra, pos(terra), "blue") e (args...)->path!(trajetoria_da_lua, pos(lua), "gray") respectivamente. Isso desenhará a trajetória da terra e da lua.

Object(1:500, (args...)->path!(trajetoria_da_terra, pos(terra), "blue"))
Object(1:500, (args...)->path!(trajetoria_da_lua, pos(lua), "gray"))

Faça um teste! Apague ou comente a função path! e estas duas linhas acima para ver o que acontece. Spoiler: Não haverá mais o desenho da trajetória em nossa simulação. Va em frente e teste!

Finalmente, o comando render, renderiza todos os objetos definidos no video que definimos como myvideo e o produz como um arquivo gif.

render(myvideo; pathname="orbitas.gif")

Agora sim, copie e cole o código em um ambiente Julia e o modifique quantas vezes quiser e aprecie o resultados.

[1]	O processo de instalação de pacotes é descrito com detalhes no capítluo 3 do livro Julia com Física: Uma Introdução.

[2]	O conceito de função e sua sintaxe são descritos no capítulo 6 do livro Julia com Física: Uma Introdução.

[3]	O conceito de arrays (vetores e matrizes) é explicado em detalhe no capítulo 4 do livro Julia com Física: Uma Introdução.

[4]	O conceito de função anônima é explicado no capítulo 6 do livro Julia com Física: Uma Introdução.

Autores: Adeil Araújo e Meirivâni Oliveira
Data: 06.dez.2020

• O pacote foi desenvolvido por:

Ole Kröger
Jacob Zelko

• Referência

[1] Javis.jl

Notebook Pluto.jl

Uma opção ao notebook Jupyter é o notebook Pluto.jl. Ele foi escrito em Julia puro e é super fácil de instalar, além de ser reativo, ou seja, ao alterar uma função ou variável, ele atualiza automaticamente todas as células afetadas por essa alteração.

Nota 1: Para utilizar o Pluto.jlvocê vai precisar:

1. ter instalado o Julia em seu computador. Dê preferência a versão v1.5, por ser mais rápida;

2. ter em seu computador o sistema operacional Linux, macOS ou Windows. No Linux e macOS o Pluto.Jlfuncionará melhor;

3. ter instalado o navegador Mozilla Firefox ou Google Chrome. Certifique-se de obter a versão mais recente.

• Instalação

1. O primeiro passo é instalar o Julia em seu computador^[5];

2. Após a instalação, execute o Julia e adicione o pacote digitando:

julia> ]
(v1.5) pkg> add Pluto

A instalação demorará alguns minutos.

Essa instalação é necessária uma única vez, no entanto, sempre que for utilizar o Pluto.jl você deverá digitar:

julia> import Pluto
julia> Pluto.run()

Pronto! O Pluto.jl será aberto no seu navegador e agora só lhe resta começar.

• Exemplo do uso do Pluto.jlcom o pacote Plots.jl^[6]

Imagine que você esteja analisando um sistema massa-mola que realiza um movimento harmônico simples (MHS) descrito pelas seguintes funções:

$$x=0.2 \cdot cos(2 \cdot t+ \pi )$$ $$v=-0.4 \cdot sen(2 \cdot t+ \pi )$$ $$\alpha=-0.8 \cdot cos(2 \cdot t+ \pi )$$

Para obter os gráficos desse movimento, você precisará digitar o seguinte código:

begin
    import Pkg
    Pkg.activate(mktempdir())
end

Nota 2: Quando há várias expressões em uma célula, temos duas poções:

1. Dividir a célula de tal forma que cada célula tenha apenas uma expressão;

2. Envolver todo o código em um bloco de begin...end.

Essa ação é necessária para configurar um ambiente de pacote limpo.

Em seguida, adicione o pacote Plots ao ambiente, importe e finalmente escolha o backend plotly.

Faça CRTL+C, CRTL+V do código abaixo no Pluto.jl.

begin
    Pkg.add("Plots")
    using Plots
end

plotly()

Para obter os gráficos de cada uma dessas funções, basta seguir o que está descrito na Figura a seguir.

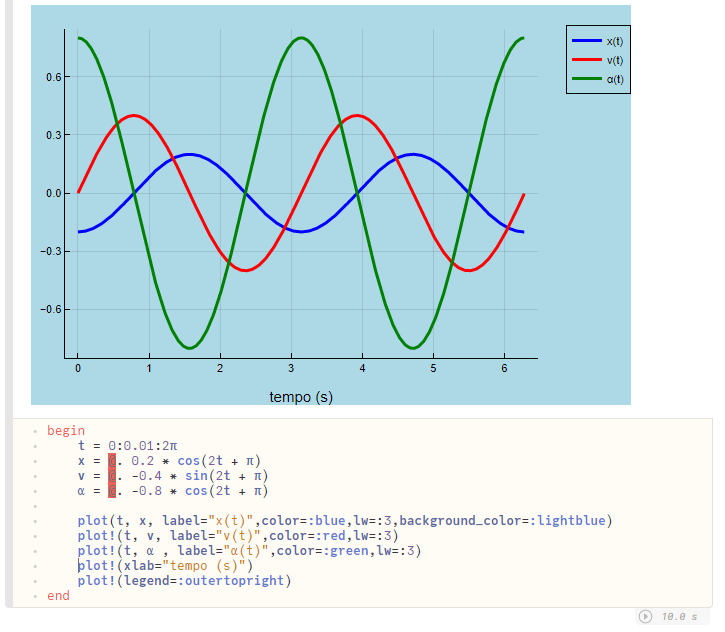
Coloquei o código abaixo para você copiar e colar noPluto.jl.

begin
    t = 0:0.01:2π
    x = @. 0.2 * cos(2t + π)
    v = @. -0.4 * sin(2t + π)
    α = @. -0.8 * cos(2t + π)
    plot(t, x, label="x(t)",color=:blue,lw=:3,background_color=:lightblue)
    plot!(t, v, label="v(t)",color=:red,lw=:3)
    plot!(t, α , label="α(t)",color=:green,lw=:3)
    plot!(xlab="tempo (s)")
    plot!(legend=:outertopright)
end

Observe que nas funções, aparece um (@.)^[7] após o sinal de igual. Ele tem a função de inserir, automaticamente, um ponto entre todos os operadores e chamadas da função.

Agora chegou a sua vez de testar o Pluto.jl. Escolha outras funções e pacotes.

[5]	O processo de instalação do Julia é descrito com detalhes no capítluo 1 do livro Julia com Física: Uma Introdução.

[6]	O uso do pacote Plots.jlé discutido em detalhes no capítluo 4 do livro Julia com Física: Uma Introdução.

[7]	O uso do (@.) é discutido em detalhes no capítluo 7, quando falamos de broadcasting, no livro Julia com Física: Uma Introdução.

• Referência

[1] Pluto.jl

Tabela Periódica - PeriodicTable.jl

Em 2019 a tabela periódica completou 150 anos. Sua primeira versão, concebida, em 1789, por Antoine Lavoisier possuía 33 elementos químicos. Hoje, ela conta com 119 elementos, organizados sistematicamente de acordo com seus números atômicos, camadas eletrônicas, número de elétrons na camada de valência e propriedades físicas.
Vários cientista contribuíram para o desenvolvimento dela, dentre eles se destaca a Física Marie Curie. Ela foi a primeira mulher a ganhar o prêmio Nobel e a primeira pessoa e única mulher a ganhá-lo por duas vezes. Um em Física ao demonstrar a existência da radioatividade natural em 1903 e outro em 1911, em Química, pela descoberta de dois novos elementos: o rádio e o polônio.

Em Julia há um pacote que nos permite acessar os elementos da tabela periódica, chama-se PeriodicTable.jl. Primeiramente precisamos instalá-lo. Para isso, basta digitar no REPL do Julia o código a seguir e pressionar Enter.

] add PeriodicTable

Caso você esteja usando o Jupyter, o procedimento é o mesmo que descrevemos na seção 3.1 do livro Julia com Física: Uma Introdução, quando falamos de instalação de pacotes. Digite:

using Pkg
Pkg.add("PeriodicTable")

Os procedimentos que descreveremos a partir de agora é o mesmo para ambos os ambientes.

Para obter acesso ao banco de dados do PeriodicTable.jlcontendo os elementos da tabela periódica, digitamos o seguinte trecho de código:

julia> using PeriodicTable

julia> elements
Elements(…119 elements…):
H                                                  He
Li Be                               B  C  N  O  F  Ne
Na Mg                               Al Si P  S  Cl Ar
K  Ca Sc Ti V  Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr
Rb Sr Y  Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I  Xe
Cs Ba    Hf Ta W  Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn
Fr Ra    Rf Db Sg Bh Hs Mt Ds Rg Cn Nh Fl Mc Lv Ts Og
Uue                                                   
      La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu    
      Ac Th Pa U  Np Pu Am Cm Bk Cf Es Fm Md No Lr

É possível procurar pelos elementos através de três formas. Como exemplo usaremos os elementos descobertos por Marie Skłodowska Curie: O rádio e o Polônio.

• Rádio

A busca pelo elemento rádio pode se dar por: elements["radium"], elements[:Ra] ou por elements[88], veja o código abaixo.

julia> elements["radium"]
Radium (Ra), number 88:
        category: alkaline earth metal
     atomic mass: 226.0 u
         density: 5.5 g/cm³
   melting point: 1233.0 K
   boiling point: 2010.0 K
           phase: Solid
          shells: [2, 8, 18, 32, 18, 8, 2]
e⁻-configuration: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f¹⁴ 5d¹⁰ 6p⁶ 7s²
      appearance: silvery white metallic
         summary: Radium is a chemical element with symbol Ra and atomic number 88. It is the sixth element in group 2 of the periodic table, also known as the alkaline earth metals. Pure radium is almost colorless, but it readily combines with nitrogen (rather than oxygen) on exposure to air, forming a black surface layer of radium nitride (Ra3N2).
   discovered by: Pierre Curie
          source: https://en.wikipedia.org/wiki/Radium

• Polônio

A busca pelo elemento polônio se dá da mesma maneira que fizemos anteriormente: elements["polonium"], elements[:Po] ou elements[84].

julia> elements["polonium"]
Polonium (Po), number 84:
        category: post-transition metal
     atomic mass: 209.0 u
         density: 9.196 g/cm³
      molar heat: 26.4 J/mol⋅K
   melting point: 527.0 K
   boiling point: 1235.0 K
           phase: Solid
          shells: [2, 8, 18, 32, 18, 6]
e⁻-configuration: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f¹⁴ 5d¹⁰ 6p⁴
      appearance: silvery
         summary: Polonium is a chemical element with symbol Po and atomic number 84, discovered in 1898 by Marie Curie and Pierre Curie. A rare and highly radioactive element with no stable isotopes, polonium is chemically similar to bismuth and tellurium, and it occurs in uranium ores. Applications of polonium are few.
   discovered by: Pierre Curie
          source: https://en.wikipedia.org/wiki/Polonium

Para cada elemento é listado: Categoria, massa atômica, densidade, ponto de fusão e ebulição, por quem foi descoberto, dentre outras características. Segundo seus desenvolvedores algumas informações foram (e serão) adicionadas ao longo do tempo.

• Desenvolvedores do PeriodicTable.jl

Steven G. Johnson
Jacob Wikmark
Carsten Bauer

• Referência

[1] Conheça as mulheres (esquecidas) por trás da tabela periódica

[2] 8 Elementos químicos invisíveis da tabela periódica

[3] Mundo Educação - Marie Curie

[4] JuliaPhysics - PeriodicTable.jl